۲۲ مرداد ۱۳۹۱ - ۰۹:۴۵
این گل زیبا نوروز نام دارد
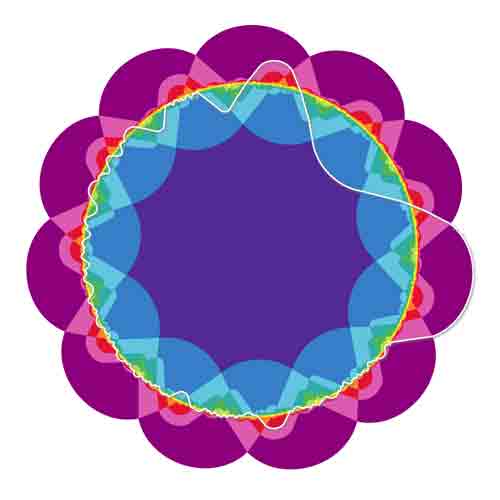
ايران اكونوميست :باغ ریاضیات شاهد شکوفایی گل جدیدی است: نموداری به نام نوروز که به شیوهای متقارن روابط میان 11 مجموعه را بیان میکند. یافتن این نمودار گلمانند نیازمند محاسباتی عظیم بود که از عهده همه کامپیوترهای روی زمین خارج است.
پوریا ناظمی: همه ما از دوران مدرسه با نمودارهای ون (Venn) آشنا هستیم. زمانی که در ریاضیات پایه تلاش میشود تا نظریه مجموعهها توضیح داده شود از این نمودارها کمک گرفته میشود. برای رسم نمودارهای ون از دایرههایی استفاده میشود که همپوشانی آنها تمامی روابط ممکن بین مجموعهها را بیان میکند. برای مثال زمانی که میخواهیم ببینیم اشتراک دو مجموعه به چه معنی است، معمولا از دو دایره استفاده میکنیم و منطقهای را که در هر دو دایره مشترک است، به عنوان اشتراک دو مجموعه هاشور زده یا رنگ میکنیم. معمولا اگر دو یا سه مجموعه با اعضای مشخص داشته باشید، روابط آنها با هم را میتوانید به راحتی به کمک این نمودارها بیان کنید؛ اما زمانی که تعداد مجموعههای شما افزایش مییابد، با توجه به اعضای هر مجموعه نمایش هندسی این روابط با مشکل مواجه میشود و گاهی برای اینکه بتوانید همپوشانیهای مناسبی پیدا کنید، ناچار خواهید شد تقارن شکل را بر هم زده و به جای دایره از بیضی یا دایرههای کشیده و یا حتی شکلهایی مثل نعل اسب برای بیان محموعه مورد نظر خود استفاده کنید.
به گزارش نیوساینتیست، چنین کاری شبیه به بازی ژیمناستیک در زمین هندسه است و چنین نمایشی برای ریاضیدان و منطقدان انگلیسی، جان ون که در سال 1880/1259 این نمودارها را خلق کرد نیز خوشآیند نبود؛ چراکه هدف اصلی از ارایه چنین نمودارهایی این بود که بتوانند درک روابط را سادهتر کنند و نه اینکه بر پیچیدگی ماجرا بیفزایند.
ریاضیدانان اما به دنبال نمودارهایی از این دست هستند که بتوانند آنها را به شکل متقارنی رسم کنند تا درک آنها سادهتر شود. آنها توانستند ثابت کنند که چنین تقارنی در نمودارهای ون تنها زمانی به وجود میآید که بخواهند رابطه میان مجموعههایی را نشان دهند که تعداد آنها عددی اول باشد. برای اینکه چنین نمودارهایی تا حد امکان خالص باشند باید در نهایت سادگی بتوان آنها را رسم کرد و معنی آن این است که در هیچ نقطهای از آن بیش از دو منحنی همدیگر را قطع نکنند.
پنجمین عدد اول
تا پیش از این نمودارهای متقارن ون تنها برای 5 و 7 مجموعه پیدا شده بود. اکنون خالق مَمَکانی و فرانک راسکی از دانشگاه ویکتوریا در بریتیش کلمبیا در کانادا موفق شدهاند این نمودار را برای حالتی از 11 مجموعه تصویر کنند.
یکی از این مجموعهها با رنگ سفید مشخص شده و رنگهای دیگر متناسب با تعداد همپوشانی مجموعه های دیگر هستند. این تیم محصول خود را نوروز (NEWROZ) نام نهادهاند. علاوه بر اینکه این نام در ایران به معنی روز نو و سال نو ایرانیان است، از نظر آوایی به New Rose یا رُز جدید نیز تشابه دارد که به ظاهر گل مانند این نمودار اشاره دارد.
برای پیدا کردن چنین نمودار گل مانندی، طراحان باید با نمودارهای بالقوه زیادی سر و کله میزدند. غربال کردن همه پتانسیلها و حالتهای مختلف ممکن برای یافتن چنین حالت خاصی و آن هم زمانی که با یک دیاگرام 11 مجموعهای سر و کار دارید، نیازمند محاسباتی بود که حتی از عهده کل کامپیوترهای زمین نیز خارج است، به همین دلیل محققان این طرح میدان جستجوی خود را تنها بین مجموعههایی محدود کردند که دارای خاصیت ویژه ای به نام تقارن تقاطع (crosscut symmetry) بودند. این خاصیت به این معنی است که یک قطعه از هر مجموعه، همه مجموعه های دیگر را دقیقا یک بار قطع کند.
چنین رویکردی برای پیدا کردن نمودارهای متقارن 7 مجموعهای نیز به کار گرفته شده بود، اما محققان میدانند که تضمینی برای موفقیت در این راه وجود ندارد. راسکی در این باره میگوید: «بعد از این همه مدتی که دنبال آنها میگردیم شگفتی بزرگ برای ما این بود حداقل یک مورد از آن را پیدا کنیم»
پیتر کامرون، ریاضیدان دانشگاه کویینمری لندن نیز در این باره میگوید: «موفقیت روشی که به منجر به پیدا کردن نوروز شده است، این ایده را تقویت میکند که میتوان از این روش برای جستجوی اجرام هندسی پیچیده دیگر نیز استفاده کرد».
با این وجود در زمان حاضر به نظر نمیرسد خود نمودار کاربردی فوری برای ریاضیدانان داشته باشد! کامرون در این باره میگوید: «ما از نمودارهای 2 و 3 مجموعهای ون برای حل معماهای ساده منطقی استفاده میکنیم، اما فراتر از آن فکر نکنم کسی غیر از هندسهدانان پیشرو کاربردی برای این نمودار سراغ داشته باشد.»
گزارش خطا

